DIEGO VALSESIA

Sampling of graph signals via randomized local aggregations

IEEE Transactions on Signal and Information Processing over Networks, June 2019

Abstract

https://ieeexplore.ieee.org/abstract/document/8457237/

Sampling of signals defined over the nodes of a graph is one of the crucial problems in graph signal processing, whereas in classical signal processing, sampling is a well-defined operation; when we consider a graph signal, many new challenges arise and defining an efficient sampling strategy is not straightforward. Recently, several works have addressed this problem. The most common techniques select a subset of nodes to reconstruct the entire signal. However, such methods often require the knowledge of the signal support and the computation of the sparsity basis before sampling. Instead, in this paper, we propose a new approach to this issue. We introduce a novel technique that combines localized sampling with compressed sensing. We first choose a subset of nodes and then, for each node of the subset, we compute random linear combinations of signal coefficients localized at the node itself and its neighborhood. The proposed method provides theoretical guarantees in terms of reconstruction and stability to noise for any graph and any orthonormal basis, even when the support is not known.

Code

Code available at https://github.com/diegovalsesia/randomized-local-aggregations

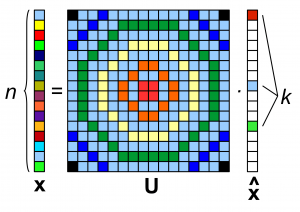
Sampling Graph Signals

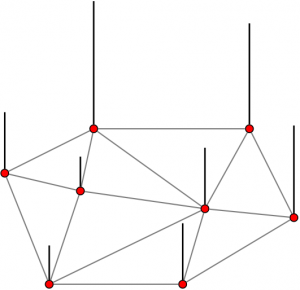
graph signal
Graph signal
  • Representing a graph signal with few measurements
  • Regularity/Low-dimensionality priors enable reconstruction (e.g. sparse support in a transform domain)
  • Locality of the sampling operation is important
    • Pointwise sampling: observing the signal value at certain nodes
    • Aggregation sampling: observing an aggregate of the signal values over a neighborhood
Pointwise sampling
Pointwise sampling
Aggregation sampling
Aggregation sampling

Randomized Local Aggregations

We know from Compressed Sensing that random projections can be used to acquire a compressed representation of a signal. Measurements acquired using Gaussian random projections enable reconstruction of signals sparse in an orthonormal basis. Reconstruction guarantees are provable if the sampling matrix satisfies the Restricted Isometry Property (RIP).

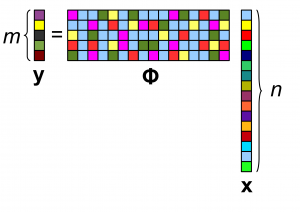
CS measurements
CS measurements
CS sparsity basis
CS sparsity basis

 

 

 

 

 

 

Issue: this sampling method is not localized if there is an underlying graph. It would require global communications throughout the graph.

Solution: randomized local aggregations.

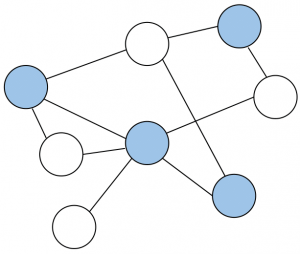
  • Define a sampling set R
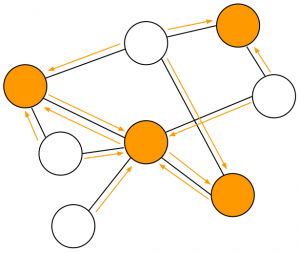
  • Aggregate the signal values in each neighborhood taking a linear combination with random weights
  • This is equivalent to having a sparse random sampling matrix with the same sparsity pattern as the adjacency matrix of the graph

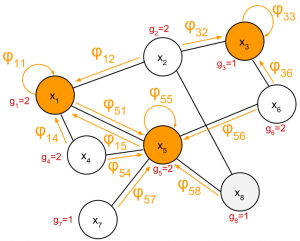
Randomized Local Aggregations

Randomized Local Aggregations
Randomized Local Aggregations

 

How to choose the sampling set? A sufficient condition…

  • Choose R to be a superset of a dominating set of the graph
  • If the dominating set is larger than the desired number of measurements: use multi-hop aggregations instead of a single-hop
  • If the dominating set is smaller than the desired number of measurements:
    • either draw a new set of random coefficients to compute a new measurement for some nodes of the domination set
    • or select some more nodes not previously chosen

Results

RIP Random Aggregations

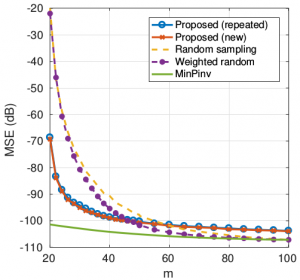
  • RIP ensures reconstruction with unknown support and stability to noise (provided enough measurements)
  • Good performance without complex optimization of the node sampling set as in some pointwise sampling algorithms. Reconstruction with known signal support with noise:
MSE as function of number of measurements. Sensor graph (n=100, k=20, noise std dev. 1e-5), bandlimited signal.
  •  It can also deal with unknown signal support:

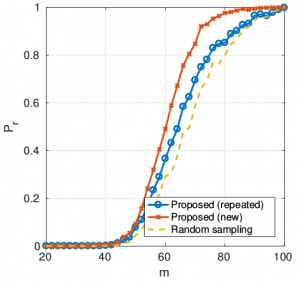
    Probability of perfect reconstruction as function of number of measurements. Sensor graph (n=100, k=20). Bandlimited signal.

 

Conclusions

Sampling graph signals with randomized local aggregations:

  • localized aggregation sampling method for graph signals;
  • theoretical guarantees of perfect reconstruction with known and unknown support;
  • stable in presence of noise
  • does not require transform basis (e.g. GFT) at sampling time

Leave a Reply

Your email address will not be published. Required fields are marked *